Probing the spacetime of Sgr A* with pulsar timing
The discovery of a pulsar in a tight orbit (orbital period of one year or less) around Sgr A* would open up unique possibilities to explore the properties of this compact object in the center of our Galaxy. The ranging capabilities provided by pulsar timing are by far superior to any resolution achievable with infrared astrometry within the foreseeable future. To give a number, a timing precision of one millisecond, which seems quite realistic (see Liu et al. 2012), corresponds to a propagation distance of 300 kilometers. As a comparison, in astrometry a distance of 300 km at the Galactic center corresponds to an angle of about 0.2 nano arcseconds, which is 50000 times smaller than the anticipated accuracy of GRAVITY. Such a precision would lead to a determination of the properties of the spacetime of Sgr A* with unprecedented precision, and help to test whether Sgr A* is indeed a Kerr black hole as predicted by general relativity (GR).

Fig. 1. Posterior likelihood of measuring the spin and quadrupole moment of Sgr A* using pulsar timing. The solid blue curve shows the expected relation between the spin and the quadrupole moment in the Kerr metric. The dashed contours (left plot) indicate the 68% and 95% confidence limits. The simulation assumes a timing precision of 100 μs for a pulsar in a 0.5-year orbit with eccentricity 0.8. Depending on the external perturbations by other masses in the vicinity of Sgr A*, one might not be able to use the full orbit for a no-hair theorem test. Nevertheless, the pulsar motion near periapsis contains enough information to extract useful constraints on the spin and quadrupole moment. Taken from Psaltis et al. (2016).
A ranging capability of just a few hundred kilometers for an orbit around Sgr A* is extremely precise, even when compared to changes in the orbit of the pulsar due to relativistic effects. Just to give an example, let’s assume a pulsar in an orbit of 0.5 years with an eccentricity of 0.8. The apsidal line of such an orbit precesses by 1.24 degrees per revolution, and consequently the location of closest approach to Sgr A*, i.e. the periapsis, moves by about 130 million kilometers per year. The dragging of the inertial frames due to the rotation of Sgr A* leads to the Lense-Thirring precession of the orbital nodes. For the orbit under consideration here they shift by several million kilometers every year. While the pulsar moves along its 0.5-year orbit in the curved spacetime of Sgr A*, its proper time is subject to a changing time dilation. A consequence of this is that an observer on Earth sees the “pulsar clock” periodically alternate between being slow and being fast with an amplitude of about 28 seconds, which is way larger than even a pessimistic timing precision. But not only the pulsar in its motion is affected by the curved spacetime of Sgr A*, also the photons propagating towards Earth do suffer a delay (Shapiro delay). For a 0.5-year orbit with an eccentricity of 0.8 the Shapiro delay leads to periodic variations in the arrival time of the pulsar signals on Earth which is at least 90 seconds (face-on configuration). For a pulsar seen nearly edge-on, the Shapiro delay can easily cause variations of many minutes in the pulse arrival times.
A detailed analysis shows that, in an ideal situation, the different relativistic effects, like periapsis precession, time dilation, and Shapiro delay, should allow to estimate the mass of Sgr A* with a fractional precision of better than 0.001% (see Wex & Kopeikin 1999, Liu et al. 2012). The spin and quadrupole moment would be known within a few percent or even better. A big uncertainty, however, comes from external perturbations by nearby masses. To some extent pulsar timing provides possibilities to mitigate such effects, by utilizing only timing measurements around the periapsis passage, where GR effects are expected to dominate over external perturbations. Figure 1 below show the results of mock data simulations which illustrate this.
Combining pulsar tests with the EHT imaging and the astrometry of stars
Imaging, the observation of stars, and the timing of a pulsar are three different experiments to probe the spacetime of Sgr A*. The correlations and degeneracies in each method are along different directions in the parameter space, and each of these methods is subject to different biases.
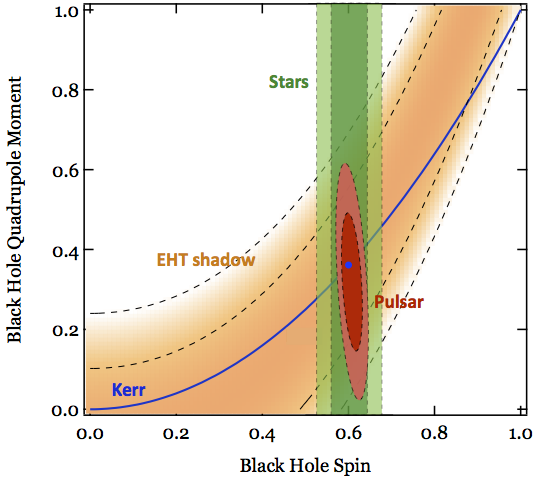
Fig. 2. Comparison of the posterior likelihood of measuring the spin and quadrupole moment of Sgr A* using the orbits of two stars (green), timing of three periapsis passages of a low-precision pulsar (red), and the shape of its shadow (gold). The solid curve shows the expected relation between these two quantities for the Kerr metric. The filled circle marks the spin and quadrupole moment of Kerr black hole assumed in the mock data simulations. See Psaltis et al. (2016) for details.rent biases.
Furthermore, these methods probe the spacetime of Sgr A* in different regimes. While pulsars and stars are only expected to be found in the far-field region (size of the orbit >> Schwarzschild radius), it is the imaging that provides the information on the near-horizon properties of the supermassive black hole. It is therefore expected that an accurate, quantitative test of the gravitational no-hair theorem requires a combination of these three types of observations. Figure 2 illustrates the different constraints one can expect from stars, a pulsar and the EHT shadow for a Kerr black hole that rotates at 60% of its maximum spin. As one can see, in contrast to the stars or the pulsar, the EHT image does not provide much constraints on the spin.

Artist’s impression of a pulsar in orbit around Sgr A*. The pulsar orbits the black hole in its far-field region, and therefore provides complementary information about the spacetime of Sgr A* when compared to the image of the shadow.